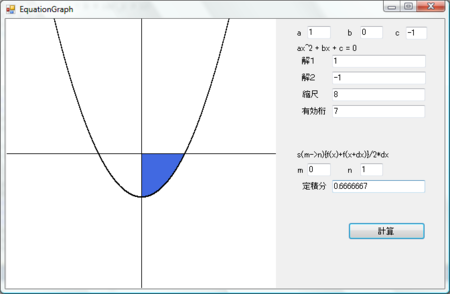
二次方程式シミュレーターに定積分を搭載。しかし倍制度浮動小数点数(double)の計算誤差で有効桁小数点以下3までしかマトモなものができない。これ半日で出来ると思ってたけど難問だな。桁を増やすと計算負荷が大きくなって待ち時間が出るので計算機としては使い辛くなる。考えものだ。
定積分を復習して分かった事はsf(x)dxのdxて「xを微分する」という意味で数ではないのね。例えば1/3「いちわるさん」と1/3「三分の一」の関係のように、答えをネストしているだけで、答えになってないようなもの。微分するという事は「細かく分ける」ということで「細かくってどのくらいよ」という問いにリーマン定数は「無限に」と言っているのであって、じゃあ無限大で割るからゼロなのかと言うと、無限大でなく無限級数でゼロではないという、ぼんやりした輪郭をしめす数式なんよな。コンピュータでやるときはdxを0.0001くらいにして計算を始めています。
0.0001だ。えらく有効桁が少ないと思われるかもしれませんが、そんなもんです。有効桁12桁くらいの積分電卓を見た事あるけど、あれどういうプログラムなのかね?浮動小数点でなく数学用の特殊な型なんかな?まあ36歳にして高校数学がやっと分かったという情けない話なので読み流して下さい。
小数点以下7桁まで改良。
sf(x)dxがリーマン積分の公式になるが、近似計算をする時に
s(f(x)+f(x+dx)) / 2 * dx
として台形の面積の公式を利用した方が近似計算が近くなる。
これを「つたん積分」とする(誰が使うねん!)
この記事を書いたら「どうせウィキでも読んだんでしょ」という反応があったけれどウィキを超えた事が書けると判断したので自分のブログで話をしているわけです。俺はウィキに書いてあるならウィキで良いと考えるタイプなので、そういう複製記事のようなものは作りません。
あと、俺は素数の研究でたぶん世界初という発見をしたことがありますが、人生で二度も世の中に浸透している数学を超えるようなものが生み出せたのはひとえにコンピュータのおかげです。実はコンピュータを使っている人が世界初の数学的発明をするということは珍しくなく、コンピュータ黎明期における数学的発見は1日に数個とか1時間に数個というレベルでの発展をして、学校で習う数学は古典のようなもので、計算にコンピュータを使うことは研究者には常識です。
しかし日本の大学はかつて科学技術研究費で計算機を買うのは手計算を怠っているとみなされて、大学のコンピュータよりスペックが高いものが出ても買い替えられないという予算の仕組みがあったそうです。俺の場合は大学ではなく企業でプログラムを覚えたし、自宅にも最新のコンピュータがあるので恵まれているともいえるけれど、家のコンピュータは実費で買っていたので大学の研究者も欲しければ実費でも買うべきだとも思いますね。
「つたん積分」は少なくとも二次関数での実験は実績を作りましたが、広く普及するためには数学の専門家が何人も例外や矛盾が無いか検証してはじめて定理として認められるもので、俺がひとり頑張ってどうなるものでもないから、ブログなら読んでいる人にいち早く新しい発見を伝える事ができるとよろこんでの投稿をしているのです。
投稿してからひとつ関数の曲線がx軸と交わるケースで交点付近の計算が近似しないため、それを考慮した新しい数式が出てくる可能性は既に分かっています。その場合でもリーマン積分より近似に正当性があると見ていますが、検算の方法をどうするかで新しい問題が出てきます。
おそらく昔の数学者は貴族のパトロン(お金出してくれる人)が居て、計算助手がたくさんいただろうという歴史研究があります。歴史に名を残す数学者は数十年に一度しか現れませんが、数学研究をしていた人の数は多くて、名が残っているのは代表者ではないかと言う説です。その計算助手がどんなに優秀でも今のコンピュータの計算量は遥か上を行くので、コンピュータで実験しながら数式の修正をするという仕事は歴史的数学者何人分もの仕事を独りでできることとなり、凡人にはどうかしらないけど天才でなくとも秀才や奇才でも充分に数学的発見をするチャンスはあるでしょう。
「ウィキ見たんじゃないの?」という2ちゃん的な野次の返しにしては長くなりましたが、そうそう簡単に人の努力を無碍(むげ)にされるのもシャクなので、これくらい書いておきます。
つたん積分は
s(f(x)+f(x+dx)) / 2 * dx
という数式になります。
これは俺が何年か温めていたものだから。プログラムにはできても数式にできなくて三流大学の教授からバカにされて絶対に言い返してやろうと思ってきたものだから。